2 The predictive brain and its cybernetic origins
2.1 Predictive processing: The basics
PP starts with the assumption that in order to support adaptive responses, the brain must discover information about the external “hidden” causes of sensory signals. It lacks any direct access to these causes, and can only use information found in the flux of sensory signals themselves. According to PP, brains meet this challenge by attempting to predict sensory inputs on the basis of their own emerging models of the causes of these inputs, with prediction errors being used to update these models so as to minimize discrepancies. The idea is that a brain operating this way will come to encode (in the form of predictive or generative models) a rich body of information about the sources of signals by which it is regularly perturbed (Clark 2013).
Applied to cortical hierarchies, PP overturns classical notions of perception that describe a largely “bottom-up” process of evidence accumulation or feature detection. Instead, PP proposes that perceptual content is determined by top-down predictive signals emerging from multi-layered and hierarchically-organized generative models of the causes of sensory signals (Lee & Mumford 2003). These models are continually refined by mismatches (prediction errors) between predicted signals and actual signals across hierarchical levels, which iteratively update predictive models via approximations to Bayesian inference (see Figure 1). This means that the brain can induce accurate generative models of environmental hidden causes by operating only on signals to which it has direct access: predictions and prediction errors. It also means that even low-level perceptual content is determined via cascades of predictions flowing from very general abstract expectations, which constrain successively more fine-grained predictions.
Two further aspects of PP need to be emphasized from the outset. First, sensory prediction errors can be minimized either “passively”, by changing predictive models to fit incoming data (perceptual inference), or “actively”, by performing actions to confirm or test sensory predictions (active inference). In most cases these processes are assumed to unfold continuously and simultaneously, underlining a deep continuity between perception and action (Friston et al. 2010; Verschure et al. 2003). This process of active inference will play a key role in much of what follows. Second, predictions and prediction errors in a Bayesian framework have associated precisions (inverse variances, Figure 1). The precision of a prediction error is an indicator of its reliability, and hence can be used to determine its influence in updating top-down predictive models. Precisions, like mean values, are not given but must be inferred on the basis of top-down models and incoming data; so PP requires that agents have expectations about precisions that are themselves updated as new data arrive (and new precisions can be estimated). Precision expectations can therefore balance the influence of different prediction-error sources on the updating of predictive models. And if prediction errors have low (expected) precision, predictive models may overwhelm error signals (hallucination) or elicit actions that confirm sensory predictions (active inference).
A picture emerges in which cortical networks engage in recurrent interactions whereby bottom-up prediction errors are continuously reconciled with top-down predictions at multiple hierarchical levels—a process modulated at all times by precision weighting. The result is a brain that not only encodes information about the sources of signals that impinge upon its sensory surfaces, but that also encodes information about how its own actions interact with these sources in specifying sensory signals. Perception involves updating the parameters of the model to fit the data; action involves changing sensory data to fit (or test) the model; and attention corresponds to optimizing model updating by giving preference to sensory data that are expected to carry more information, which is called precision weighting (Hohwy 2013). This view of the brain is shamelessly model-based and representational (though with a finessed notion of representation), yet it also deeply embeds the close coupling of perception and action and, as we will see, the importance of the body in the mediation of this interaction.
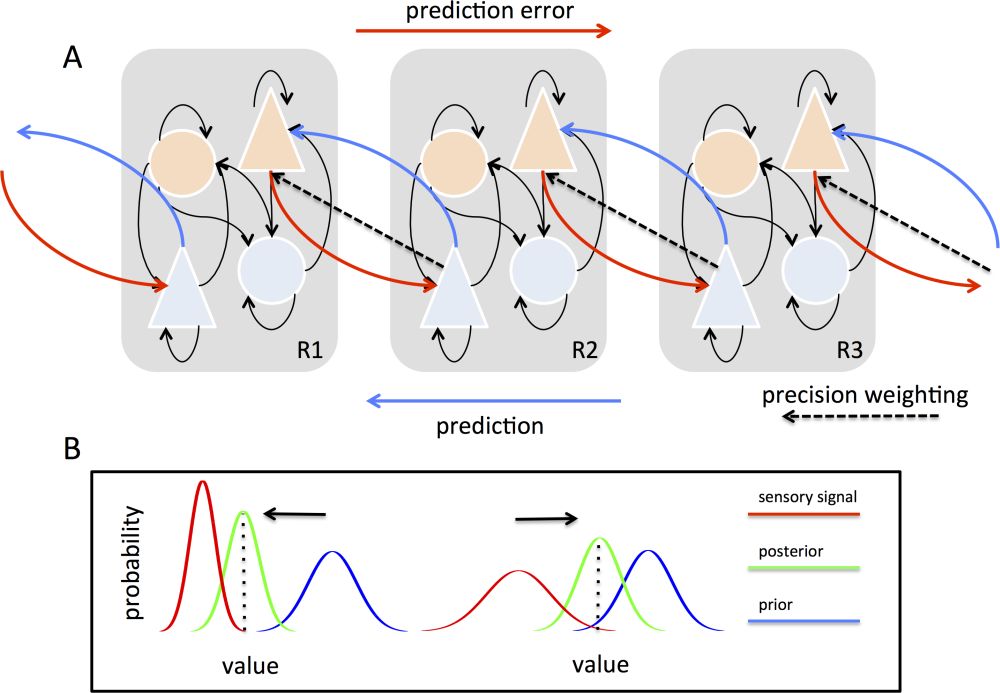Figure 1: A. Schemas of hierarchical predictive coding across three cortical regions; the lowest on the left (R1) and the highest on the right (R3). Bottom-up projections (red) originate from “error units” (orange) in superficial cortical layers and terminate on “state units” (light blue) in the deep (infragranular) layers of their targets; while top-down projections (dark blue) convey predictions originating in deep layers and project to the superficial layers of their targets. Prediction errors are associated with precisions, which determine the relative influence of bottom-up and top-down signal flow via precision weighting (dashed lines). B. The influence of precisions on Bayesian inference and predictive coding. The curves show probability distributions over the value of a sensory signal (x-axis). On the left, high precision-weighting of sensory signals (red) enhances their influence on the posterior (green) and expectation (dotted line) as compared to the prior (blue). On the right, low sensory precision weighting has the opposite effect. Figure adapted from Seth (2013).
2.2 Predictive processing and the free energy principle
PP can be considered a special case of the free energy principle, according to which perceptual inference and action emerge as a consequence of a more fundamental imperative towards the avoidance of “surprising” events (Friston 2005, 2009, 2010). On the free energy principle, organisms – by dint of their continued survival—must minimize the long-run average surprise of sensory states, since surprising sensory states are likely to reflect conditions incompatible with continued existence (think of a fish out of water). “Surprise” is not used here in the psychological sense, but in an information-theoretic sense—as the negative log probability of an event’s occurrence (roughly, the unlikeliness of the occurrence of an event).
The connection with PP arises because agents cannot directly evaluate the (information-theoretic) surprise associated with an event, since this would require—impossibly—the agent to average over all possible occurrences of the event in all possible situations. Instead, the agent can only maintain a lower limit on surprise by minimizing the difference between actual sensory signals and those signals predicted according to a generative or predictive model. This difference is free energy, which, under fairly general assumptions, is the long-run sum of prediction error.
An attractive feature of the free energy principle is that it brings to the table a rich mathematical framework that shows how PP can work in practice. Formally, PP depends on established principles of Bayesian inference and model specification, whereby the most likely causes of observed data (posterior) are estimated based on optimally combining prior expectations of these causes with observed data, by using a (generative, predictive) model of the data that would be observed given a particular set of causes (likelihood). (See Figure 1 for an example of priors and posteriors.) In practice, because optimal Bayesian inference is usually intractable, a variety of approximate methods can be applied (Hinton & Dayan 1996; Neal & Hinton 1998). Friston’s framework appeals to previously worked-out “variational” methods, which take advantage of certain approximations (e.g., Gaussianity, independence of temporal scales)—thus allowing a potentially neat mapping onto neurobiological quantities (Friston et al. 2006).[1]
The free energy principle also emphasizes action as a means of prediction error minimization, this being active inference. In general, active inference involves the selective sampling of sensory signals so as to minimize uncertainty in perceptual hypotheses (minimizing the entropy of the posterior). In one sense this means that actions are selected to provide evidence compatible with current perceptual predictions. This is the most standard interpretation of the concept, since it corresponds most directly to minimization of prediction error (Friston 2009). However, as we will see, actions can also be selected on the basis of an attempt to find evidence going against current hypotheses, and/or to efficiently disambiguate between competing hypotheses. These finessed senses of active inference represent developments of the free energy framework. Importantly, action itself can be thought of as being brought about by the minimization of proprioceptive prediction errors via the engagement of classical reflex arcs (Adams et al. 2013; Friston et al. 2010). This requires transiently low precision-weighting of these errors (or else predictions would simply be updated instead), which is compatible with evidence showing sensory attenuation during self-generated movements (Brown et al. 2013).
A more controversial aspect of the free energy principle is its claimed generality (Hohwy this collection). At least as described by Friston, it claims to account for adaptation at almost any granularity of time and space, from macroscopic trends in evolution, through development and maturation, to signalling in neuronal hierarchies (Friston 2010). However, in some of these interpretations reliance on predictive modelling is only implicit; for example the body of a fish can be considered to be an implicit model of the fluid dynamics and other affordances of its watery environment (see section 2.3). I am not concerned here with these broader interpretations, but will focus on those cases in which biological (neural) mechanisms plausibly implement explicit predictive inference via approximations to Bayesian computations—namely, the Bayesian brain (Knill & Pouget 2004; Pouget et al. 2013). Here, the free energy principle has potentially the greatest explanatory power, especially given the convergence of empirical evidence (see Clark 2013 and Hohwy 2013 for reviews) and computational modelling showing how cortical microcircuits might implement approximate Bayesian inference (Bastos et al. 2012).
2.3 Predictive processing, free energy, and cybernetics
Typically, the origins of PP are traced to the work of the 19th Century physiologist Hermann von Helmholtz, who first formalized the idea of perception as inference. However, the Helmholtzian view is rather passive, inasmuch as there is little discussion of active inference or behaviour. The close coupling of perception and action emphasized in the free energy principle points instead to a deep connection between PP and mid-twentieth-century cybernetics. This is most obvious in the works of W. Ross Ashby (Ashby 1952; 1956; Conant & Ashby 1970) but is also evident more generally (Dupuy 2009; Pickering 2010). Importantly, cybernetics adopted as its central focus the prediction and control of behaviour in so-called teleological or purposeful machines.[2] More precisely, cybernetic theorists were (are) interested in systems that appear to have goals (i.e., teleological) and that participate in circular causal chains (i.e., involving feedback) coupling goal-directed sensation and action.
Two key insights from the first wave of cybernetics usefully anticipate the core developments of PP within cognitive science. These are both associated with Ashby, a key figure in the movement and often considered its leader, at least outside the USA (Figure 2).
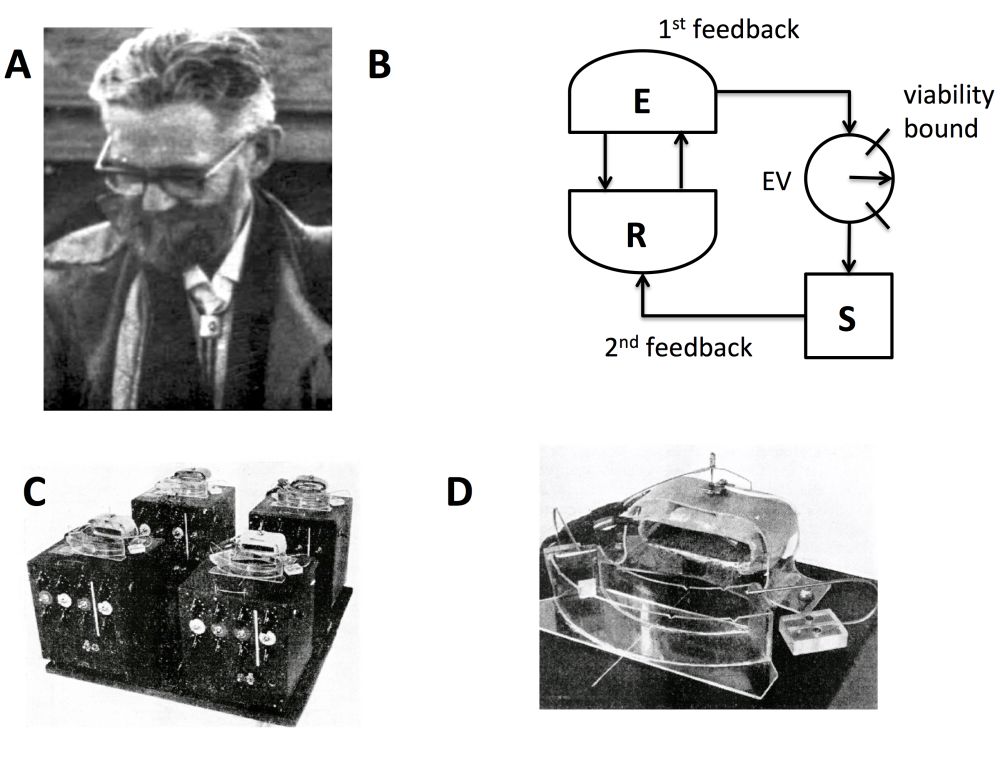Figure 2: A. W. Ross Ashby, British psychiatrist and pioneer of cybernetics (1903–1972). B. A schematic of ultrastability, based on Ashby’s notebooks. The system R homeostatically maintains its essential variables (EVs) within viability limits via first-order feedback with the environment E. When first-order feedback fails, so that EVs run out-of-bounds, second order “ultrastable” feedback is triggered so that S (an internal controller, potentially model-based) changes the parameters of R governing the first-order feedback. S continually changes R until homeostatic relations are regained, leaving the EVs again within bounds. C. Ashby’s “homeostat”, consisting of four interconnected ultrastable systems, forming a so-called “multistable” system. D. One ultrastable unit from the homeostat. Each unit had a trough of water with an electric field gradient and a metal needle. Instability was represented by the non-central needle positions, which on occurring would alter the resistances connecting the units via discharge through capacitors. For more details see Ashby (1952) and Pickering (2010).
The first insight consists in an emphasis on the homeostasis of internal essential variables, which, in physiological settings, correspond to quantities like blood pressure, heart rate, blood sugar levels, and the like. In Ashby’s framework, when essential variables move beyond specific viability limits, adaptive processes are triggered that re-parameterize the system until it reaches a new equilibrium in which homeostasis is restored (Ashby 1952). Such systems are, in Ashby’s terminology, ultrastable, since they embody (at least) two levels of feedback: a first-order feedback that homeostatically regulates essential variables (like a thermostat) and a second-order feedback that allostatically[3] re-organises a system’s input–output relations when first-order feedback fails, until a new homeostatic regime is attained. In the most basic case, as implemented in Ashby’s famous “homeostat” (Figure 2), this second-order feedback simply involves random changes to system parameters until a new stable regime is reached. The importance of this insight for PP is that it locates the function of biological and cognitive processes in generalizing homeostasis to ensure that internal essential variables remain within expected ranges.
Another way to summarize the fundamental cybernetic principle is to say that adaptive systems ensure their continued existence by successfully responding to environmental perturbations so as to maintain their internal organization. This leads to the second insight, evident in Ashby’s law of requisite variety. This states that a successful control system must be capable of entering at least as many states as the system being controlled: “only variety can force down variety” (Ashby 1956). This induces a functional boundary between controller and environment and implies a minimum level of complexity for a successful controller, which is determined by the causal complexity of the environmental states that constitute potential perturbations to a system’s essential variables. This view was refined some years later, in a 1970 paper written with Roger Conant entitled “Every good regulator of a system must be a model of that system” (Conant & Ashby 1970). This paper builds on the law of requisite variety by arguing (and attempting to formally show) that the nature of a controller capable of suppressing perturbations imposed by an external system (e.g., the world) must instantiate a model of that system. This provides a clear connection with the free energy principle, which proposes that adaptive systems minimize a limit on free energy (long-run average surprise) by inducing and refining a generative model of the causes of sensory signals. It also moves beyond Ashby’s homeostat by implying that model-based controllers can engage in more successful multi-level feedback than is possible by random variation of higher-order parameters.
Putting these insights together provides a distinctive way of seeing the relevance of PP to cognition and biological adaptation. It can be summarized as follows. The purpose of cognition (including perception and action) is to maintain the homeostasis of essential variables and of internal organization (ultrastability). This implies the existence of a control mechanism with sufficient complexity to respond to (i.e., suppress) the variety of perturbations it encounters (law of requisite variety). Further, this structure must instantiate a model of the system to be controlled (good regulator theorem), where the system includes both the body and the environment (and their interactions). As Ashby himself tells us “[t]he whole function of the brain can be summed up in: error correction” (quoted in Clark 2013, p. 1). Put this way, perception emerges as a consequence of a more fundamental imperative towards organizational homeostasis, and not as a stage in some process of internal world-model construction. This view, while highlighting different origins, closely parallels the assumptions of the free energy principle in proposing a primary imperative towards the continued survival of the organism (Friston 2010).
It may be surprising to consider the legacy of cybernetics in this light. This is because many previous discussions of this legacy focus on examples which show that complex, apparently goal-directed behaviour can emerge from simple mechanisms interacting with structured bodies and environments (Beer 2003; Braitenberg 1984). On this more standard development, cybernetics challenges rather than asserts the need for internal models and representations: it is often taken to justify slogans of the sort “the world is its own best model” (Brooks 1991). In fact, cybernetics is agnostic with respect to the need for deployment of explicit internally-specified predictive models. If environmental circumstances are reasonably stable, and mappings between perturbations and (homeostatic) responses reasonably straightforward, then the good regulator theorem can be satisfied by controllers that only implicitly model their environments. This is the case, for instance, in the Watt governor: a device that is able exquisitely to control the output of (for instance) a steam engine, in virtue of its mechanism, and not through the deployment of explicit predictive models or representations (see Figure 3 and Van Gelder 1995; note that the governor can be described as an implicit model since it has variables – e.g., eccentricity of the metal balls from the central column – which map onto environmental variables that affect the homeostatic target – engine output). However, where there exist many-to-many mappings between sensory states and their probable causes, as may be the case more often than not, it will pay to engage explicit inferential processes in order to extract the most probable causes of sensory states, insofar as these causes threaten the homeostasis of essential variables.
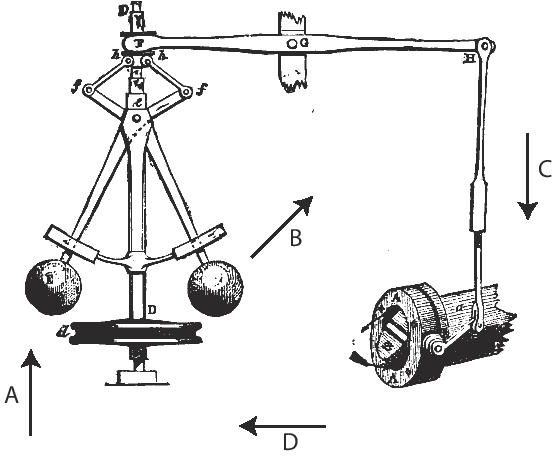Figure 3: The Watt governor. This system, a central contributor to the industrial revolution, enabled precise control over the output of (for example) steam engines. As the speed of the engine increases, power is supplied to the governor (A) by a belt or chain, causing it to rotate more rapidly so that the metal balls have more kinetic energy. This causes the balls to rise (B), which closes the throttle valve (C), thereby reducing the steam flow, which in turn reduces engine speed (D). The opposite happens when the engine speed decreases, so that the governor maintains engine speed at a precise equilibrium.
In summary, rather than seeing PP as originating solely in the Helmholtzian notion of “perception as inference”, it is fruitful to see it also as part of a process of model-based predictive control entailed by a fundamental imperative towards internal homeostasis. This shift in perspective reveals a distinctive agenda for PP in cognitive science, to which I shall now turn.