4 Mapping and decoding
It seems a different, more direct, and generic approach is necessary in order to identify the neural correlates of the contents of consciousness. It may help to start in the simplest possible way. If we want to explain the occurrence of a conscious experience E1 with the occurrence of a brain state B1 then—roughly speaking—the experience and the brain state should always happen together. If we want to explain N experiences E1…N with brain states, we will need N different brain states B1…N in order to encode the different experiences. If brain data from a specific area only adopts one of five states every time a participant has one of ten experiences it is impossible to explain the experiences through the different brain states. Ultimately this boils down to a mapping problem (Haynes 2009; Figure 3).
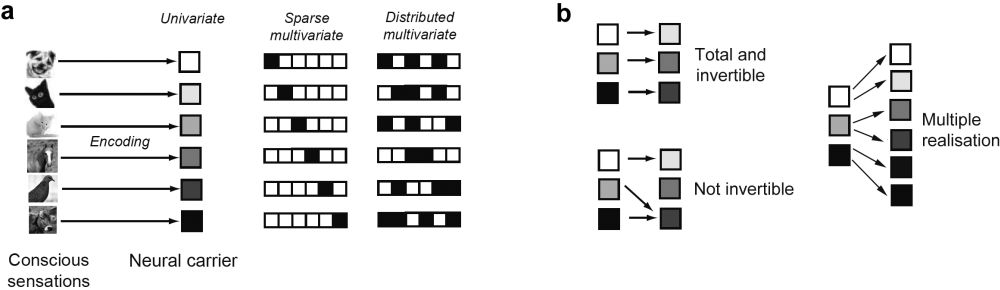 Figure 3: Principles of mapping between mental states and brain states (see text; adapted from Haynes2009 with additional images from Wikipedia).
Figure 3: Principles of mapping between mental states and brain states (see text; adapted from Haynes2009 with additional images from Wikipedia).
A set of conscious sensations, here visual percepts of six different animals, can be encoded in a neural carrier in multiple ways. Three principles are illustrated in Figure 3a. One hypothetical way to code these six animals would be to use a single neuron and to encode the objects by the firing rates of this neuron. One would assign one specific firing rate to each of the different animals, say 1Hz to the dog, 2Hz to the cat and 3Hz to the mouse, etc. This approach is also referred to as a univariate code, because it uses only one single parameter of neural activity. It has the advantage of requiring only a single neuron. In principle it is possible to encode many different objects with a single neuron. The idea would be very similar to a telephone number, if one thinks of different numbers corresponding to different firing rates. In theory it would be possible to encode every single telephone in the world in this way, provided that the firing rates could be established very precisely and reliably. The disadvantage with this approach—even if firing rates could be established with great precision—is that it can only handle exclusive thoughts, i.e. it has no way of dealing with a superposition of different animals, say a cat together with a dog.
A different approach is not to use a single neuron to encode different thoughts, but instead to use a set of neurons to encode a set of thoughts. This population-based approach is also termed “multivariate”. One way to encode thoughts about six different animals would be to assign one specific neuron to the occurrence of each thought. Neuron one, say, might fire when a person thinks about a dog; neuron two would fire when they were thinking about a cat, etc. Here the firing rate is irrelevant; only a threshold is needed, such that one has a way of deciding when a neuron is “active” or “not active”. This specific coding scheme is variably termed “sparse code”, “labelled line code”, “cardinal cell code” or “grandmother cell code” (see e.g., Quiroga et al. 2008). It has the advantage of being able to handle arbitrary superpositions and combinations of thoughts, say thoughts about a meeting of a dog, a cat, and a mouse. A disadvantage is that a different neuron is needed for the encoding of each new entity. N neurons can only encode N different thoughts. Given that the average human brain comprises 86 billion neurons (Azevedo et al. 2009) this might not seem too big a problem. A different way to use a population of neurons to encode a set of thoughts would be a distributed multivariate code. Here, each mental state is associated with a single activation pattern in the neural population, but now arbitrary combinations of neurons are possible for the encoding of each single thought. This allows for the encoding of 2N thoughts with N neurons, if each neuron is only considered to be “on” or “off”.
There are various examples of these different types of codes. The encoding of intensity follows a univariate code: The difference between a brighter and a darker image is encoded in a higher versus a lower firing rate of the corresponding neurons in the visual cortex (see e.g., Haynes 2009). However, to date, I am not aware of any example where different higher-level interpretations of stimuli are coded in a univariate format. There are many examples of labelled line codes. The retinotopic location within the visual field is encoded in a sparse, labelled line format (e.g., Sereno et al. 1995). One position in the visual field is coded by one set of neurons in the early visual cortex; another position is encoded by a different set of neurons. If two objects appear in the visual field simultaneously, then both of the corresponding sets of neurons become active simultaneously. A similar coding principle is observed for auditory pitch, where different pitches are coded in different cells in the form of a tonotopic map (Formisano et al. 2003). The somatosensory and motor homunculi are also examples of labelled line codes, each position in the brain corresponding to one specific position in the body (Penfield & Rasmussen 1950). A distributed multivariate code is, for example, used to code different objects (Haxby et al. 2001) or different emotions (Anders et al. 2011).
When identifying the mapping between brain states and mental states one is generally interested in identifying which specific population of neurons is a suitable candidate for explaining a particular class of visual experiences. For this it is possible to formulate a number of constraints (Haynes 2009). First, the mapping needs to assign one brain state to each mental state in which we are interested. In other words, the mapping has to be total (Figure 3b). This should be easy—it just means that we can assign one measured brain state to each different mental state. Second, the mapping cannot assign the same brain state to two different mental states. Otherwise the brain states would not be able to explain the different mental states. Technically this means the mapping has to be invertible, or injective. Every brain state should be assigned to no more than one mental state. However, it is possible—in the sense of multiple realisation—that multiple brain states are assigned to the same mental state, as long as neither of these brain states co-occurs with other mental states. The brain states referred to here only mean brain states that are relevant for explaining a set of mental states. If we want to explain thoughts about six animals, say, it might not be necessary that brain states in the motor cortex are different for the different animals. However, if one wants to propose one set of neurons (say, those in the lateral occipital complex, Malach et al. 1995) as a candidate for explaining animal experiences, then this can only hold if the abovementioned mapping requirements are fulfilled.
In practice it will be very difficult to establish this mapping directly. One major problem is that we can’t measure brain states in sufficient detail with current neuroscience techniques. Non-invasive measurement techniques such as electroencepholography (EEG) or functional magnetic resonance imaging (fMRI) have very limited spatial resolution. FMRI for example resolves the brain with a measurement grid of around 1–3mm, so that each measurement unit (or voxel) contains up to a million cells. And the temporal resolution of fMRI is restricted because fMRI measures the delayed and temporally-extended hemodynamic response to neural stimulation. While it is possible—to some degree—to reconstruct visual experiences from fMRI signals (e.g., Miyawaki et al. 2008), fMRI cannot resolve temporal details of neural processes, such as the synchronized activity of multiple cells. But it is not only EEG and fMRI that have limited resolution: Invasive recording techniques are typically restricted to individual well-circumscribed locations, where surgery is performed. And even with multielectrodes it is not possible to identify the state of each individual neuron in a piece of living tissue.
Another important limitation lies in our ability to precisely characterize and cognitively penetrate phenomenal states (e.g., Raffman 1995). There is currently no psychophysical technique that would allow us to characterize the full details of a person’s visual experiences at each location in the visual field. Verbal reports or button presses can convey only a very reduced picture of the true complexity of visual experiences. So ultimately, the mapping requires precision from both psychology and neuroscience, and any imprecision in either approach will blur the mapping and distort the interpretation.
The next best option short of establishing full mapping is to use decoding techniques that follow a similar logic. Brain-based decoding is also referred to as “brain reading” or “multivoxel pattern analysis” (see Haynes & Rees 2005 for a review). The basic idea is to see to which degree it is possible to infer a mental state from a measurement of a brain state. Say you want to test whether the lateral occipital complex is a suitable candidate for encoding visual thoughts about animals. You test if it is possible to infer which animal a person is currently seeing by training a classifier to learn the association between animal and brain activation pattern, and then one needs to test whether the classifier can correctly assign the animal that belongs to a new measurement of brain activity. In the following, this approach will be explained in detail.
Take for example a hypothetical fMRI-measurement of the human brain within a three by three grid of locations, amounting to nine voxels (Figure 4a). These nine voxels can be systematically resorted into a column of numbers (or vectors), where each entry denotes the activation at one location (high values correspond to strong fMRI responses). Say one was interested in testing whether these nine voxels contain information about two different visual images, perhaps a dog and a cat. The question that needs to be addressed is whether the response patterns (i.e., the vectors) are sufficiently different to allow for distinguishing between the animals, based on these brain activity measurements alone. The vector is not a useful way to see whether this classification is possible. It can help to visualize the same information in a two-dimensional coordinate system. Take the responses to the dog. One can think of the first and second entries in the vector as x- and y-values that define points in a coordinate system. The response in the first voxel (x) to the dog is a low value (2), while the second value (y) is a high value (8). When plotted in a two-dimensional coordinate system (Figure 4b), this yields a point in the top left of the coordinate system, shown here in red. Repeated measurements of the brain response to the dog yield a small cloud of red points. Repeatedly measured brain responses to the cat have high values in voxel 1 (x) and low values in voxel 2 (y). In the two-dimensional coordinate system this yields a cloud of blue points in the bottom right of the coordinate system. Clearly the responses are separable in this two-dimensional coordinate system, so the two animals enjoy reliably separate neural representations in this set of nine voxels. In this hypothetical example, each of the two voxels alone would be sufficiently informative about the category of animal. By collapsing the points for voxel one onto the x-axis it becomes clear that the two distributions of points (red and blue) are sufficiently different to allow for telling the two apart. The same holds for voxel two by collapsing to the y-axis. This is akin to a labelled line code, with one line for “dog” and one line for “cat”.
However, there are cases where the two distributions will not be so easily separable. Figure 4c shows an example where the individual voxels do not have information about the animals. The collapsed or “marginal” distributions largely overlap. There is no way to tell a cat response from a dog response by looking at either voxel one or two alone. However, by taking into account the joint activity in both voxels, the two animals become clearly separable. Responses to the dog all cluster to the top left of the diagonal and responses to the cat cluster to its bottom right. This joint consideration of the information contained in multiple voxels is the underlying principle of multivariate decoding. The line separating the two distributions is known as the decision boundary. Decision boundaries are not necessarily straight lines. Many other types of distributions of responses are possible. Figure 4d, for example, shows a non-linear decision boundary. Finding the optimal decision boundary is the key objective in the field of machine learning (Müller et al. 2001), where many different types of classifiers have been developed (most well known are support vector classifiers). In order to identify the decision boundary the available data are split into training and test data. The test data are put aside and only the training data are then used to find a decision boundary, as, for example, is shown in Figure 4e. The crucial test is then performed with the remaining test data. The classifier is applied to these data to see to which degree it is able to correctly assign the labels. Depending on which side of the decision boundary a test data point falls upon, it will yield either a correct or an incorrect classification.
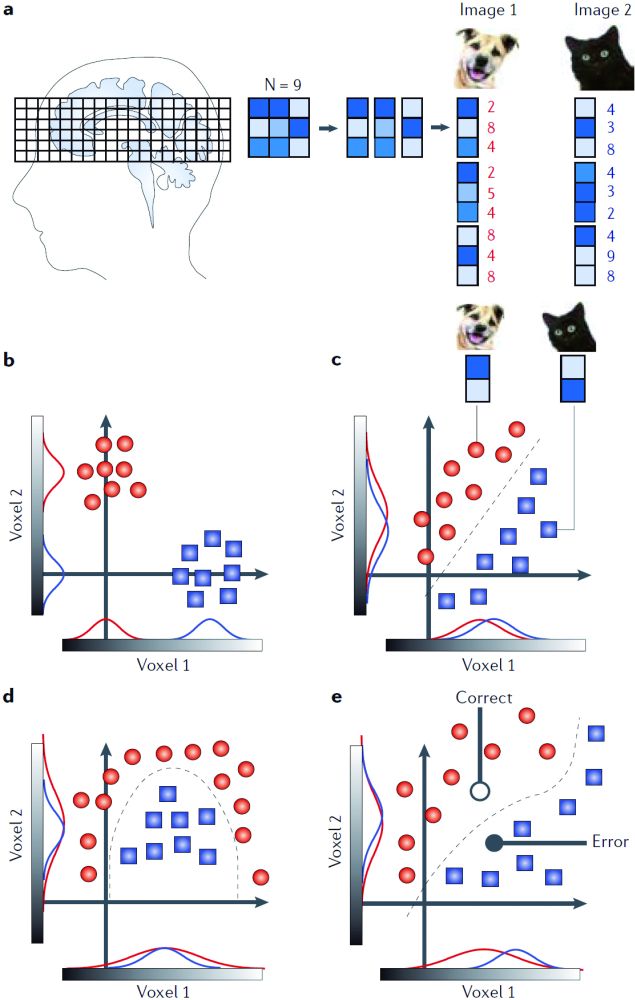 Figure 4: Mental state decoding using classification techniques (image adapted from Haynes & Rees 2005).
Figure 4: Mental state decoding using classification techniques (image adapted from Haynes & Rees 2005).
Please note the similarity between the mapping of mental states and brain states. The red cloud of points in Figure 4b shows a two-dimensional response pattern that corresponds to the neural code for percepts of dogs. The spread of the point cloud (i.e. the fact that repeated measurements don’t yield identical values) could mean two things. Either the spread reflects noise and uncertainty that is typically inherent in measurements of neural data. This could, for example, reflect the fact that single fMRI voxels can sample many thousand cells, only few of which might be involved in processing. Additionally, physiological background rhythms can influence the signals and contribute to noise (Fox et al. 2006). Alternatively, however, the spread of the points could also be an inherent property of the representation. This would suggest that every time a person sees or visual imagines a dog, a slightly different activation pattern is observed in the brain. This would then be evidence of multiple realization. Current measurement techniques do not have sufficient precision to distinguish between these two accounts. One difference between the multivariate mapping shown in Figure 3a (right) and the classification in Figure 4 is that the classification shows response distributions where each individual variable (voxel, channel) can adopt a graded value, whereas the values in Figure 3a (right) are only binary.